When Quantization Affects Confidence of Large Language Models?
NAACL 2024
Irina Proskurina
Luc Brun
Guillaume Metzler
Julien Velcin
Contributions
- We investigate how quantization with GPTQ influences the calibration and confidence of LLMs
- We assess the confidence alignment between compressed and full-precision LLMs at scale
- We explain the quantization loss from the initial confidence perspective
Introduction
Motivation
- Recent works on scaling laws have shown that emerging abilities come with the scale increase, which makes well-performing larger models less accessible and limits their practical usability
- Quantization may degrade the initial performance and amplify the sensitivity of an LLM to certain linguistic phenomena and stereotypes
- No attention has been paid to explaining the compression loss, particularly its variance across different texts
Post-training quantization
On the dataset X we want to find a quantized version of weight ˆW∗l to minimize the mean squared error:
ˆW∗l=argminˆWl||ˆWlX−WlX||22
Optimal Brain Quantization (OBQ) method state that we can quantize each row independently: ||ˆWlX−WlX||22=∑drowi=0||Wl[i,:]X−ˆW∗l[i,:]X||22
Quantization with GPTQ
- Learn the rounding operation using a small dataset
- Split weights in groups (blocks) and quantize them group-wise, using the inverse Hessian information stored
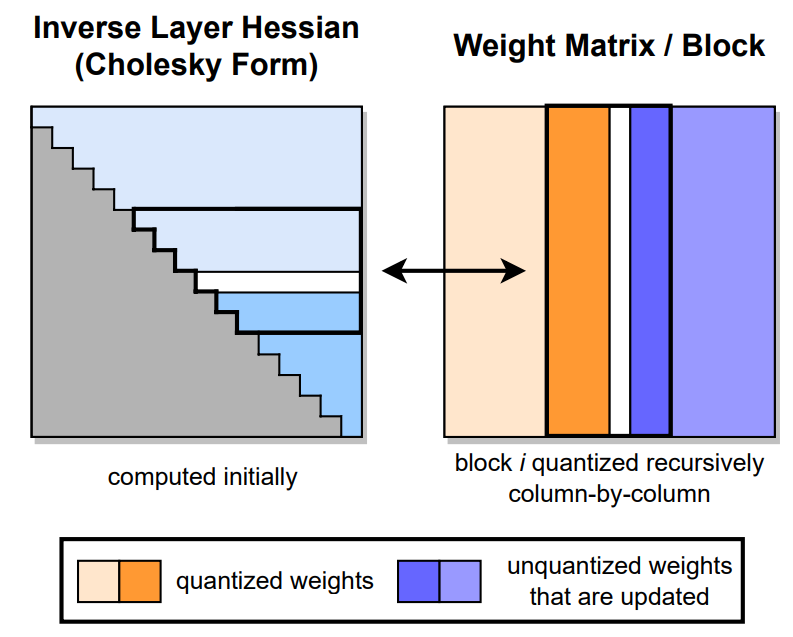
Methodology
Zero-shot Question Answering: pipeline
Data: Six standard commonsense reasoning tasks
- question answering involving reading comprehension (BoolQ)
- natural text entailment (XStory-En, HellaSwag)
- science fact knowledge (ARC, OBQA)
- physical commonsense (PIQA)
Problem
We consider a classification problem : questions x paired with candidate answers y:
ˆy=arg max y∈YpLM(y|x), where: pLM(y|x)=∏|y|i=1pLM(y[i]|x,y[1:i−1])
Calibration Metrics
Model calibrated : P(ˆY=Y|ˆp=p)=p.
Metrics used for estimating calibration error (CE):
- ECE for binary problems: ECE=∑Mm=1|Bm|n|acc(Bm)−¯conf(Bm)|
- ACE for multi-class benchmarks: ACE=1CM∑Cc=1∑Mm=1|acc(Bm,c)−¯conf(Bm,c)|
Results
Confidence Impact
| Dataset | Acc. ↑ | CE ↓ |
|---|---|---|
| ArcEasy | 81.10 (-1.18) | 7.94 (+0.83) |
| BoolQ | 83.61 (-0.86) | 38.62 (+3.13) |
| HellaSwag | 61.30 (-1.53) | 34.3 (+1.29) |
| OpenBookQA | 32.60 (-0.40) | 45.24 (+2.08) |
Zero-shot accuracy scores (Acc.) and calibration error (CE) for Mistral model. The changes of the scores after GPTQ are in brackets.
Calibration Impact
| Model | Conf. | Conferr | Conftrue | H*100 |
|---|---|---|---|---|
| Mistral | 96.85 | 95.02 | 61.14 | 10.96 |
| + GPTQ | 96.89 | 95.13 | 59.73∗ | 10.87 |
| LLaMA | 96.8 | 95.34 | 56.83 | 11.37 |
| + GPTQ | 96.48 | 95.13 | 53.69∗ | 12.21∗ |
Confidence and prediction entropy evaluation results on HellaSwag.
Cases of Confidence Change
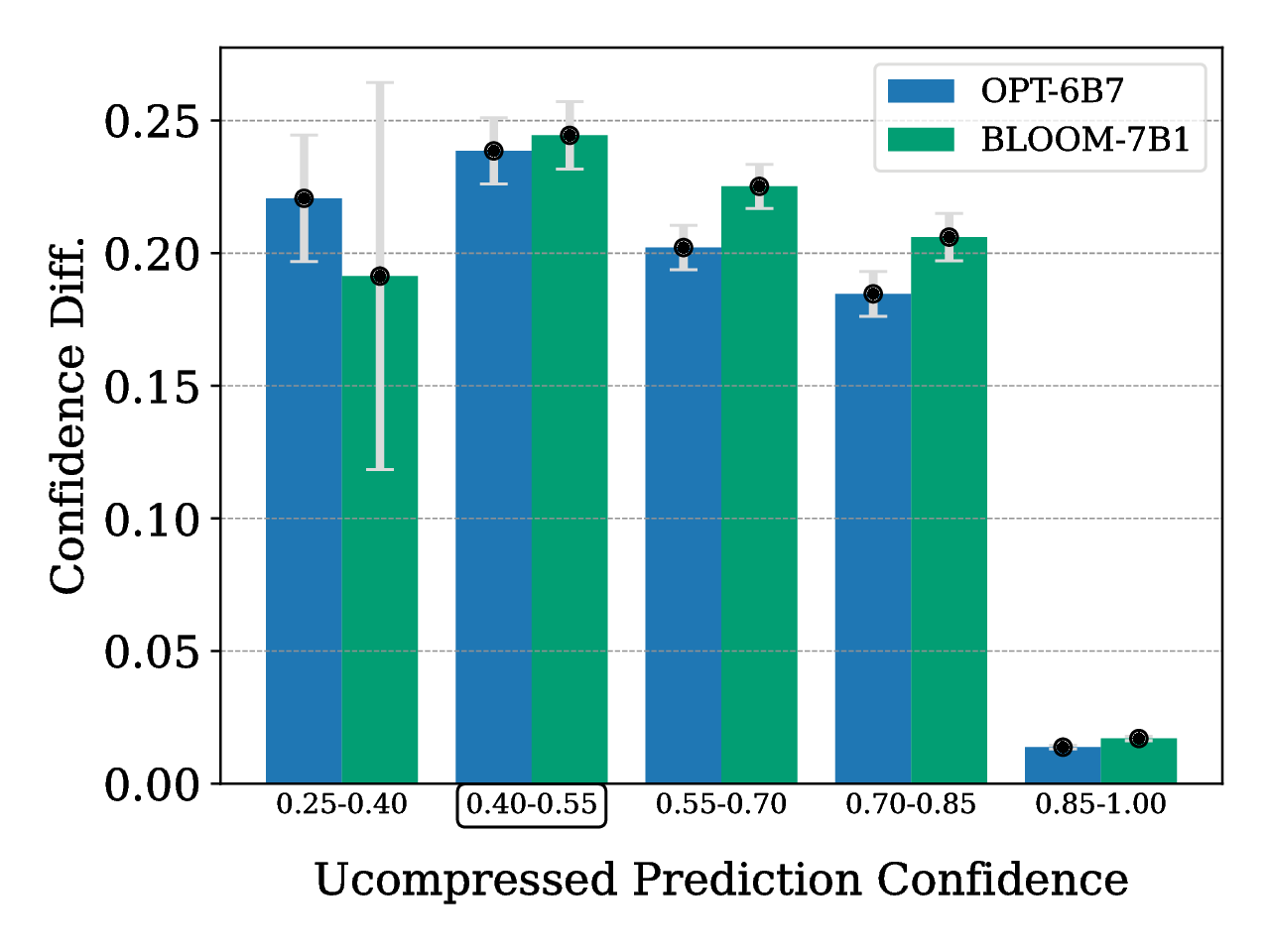
The samples with lower pre-quantization confidence level are the more affected by the quantization process
Jensen-Shannon Distances
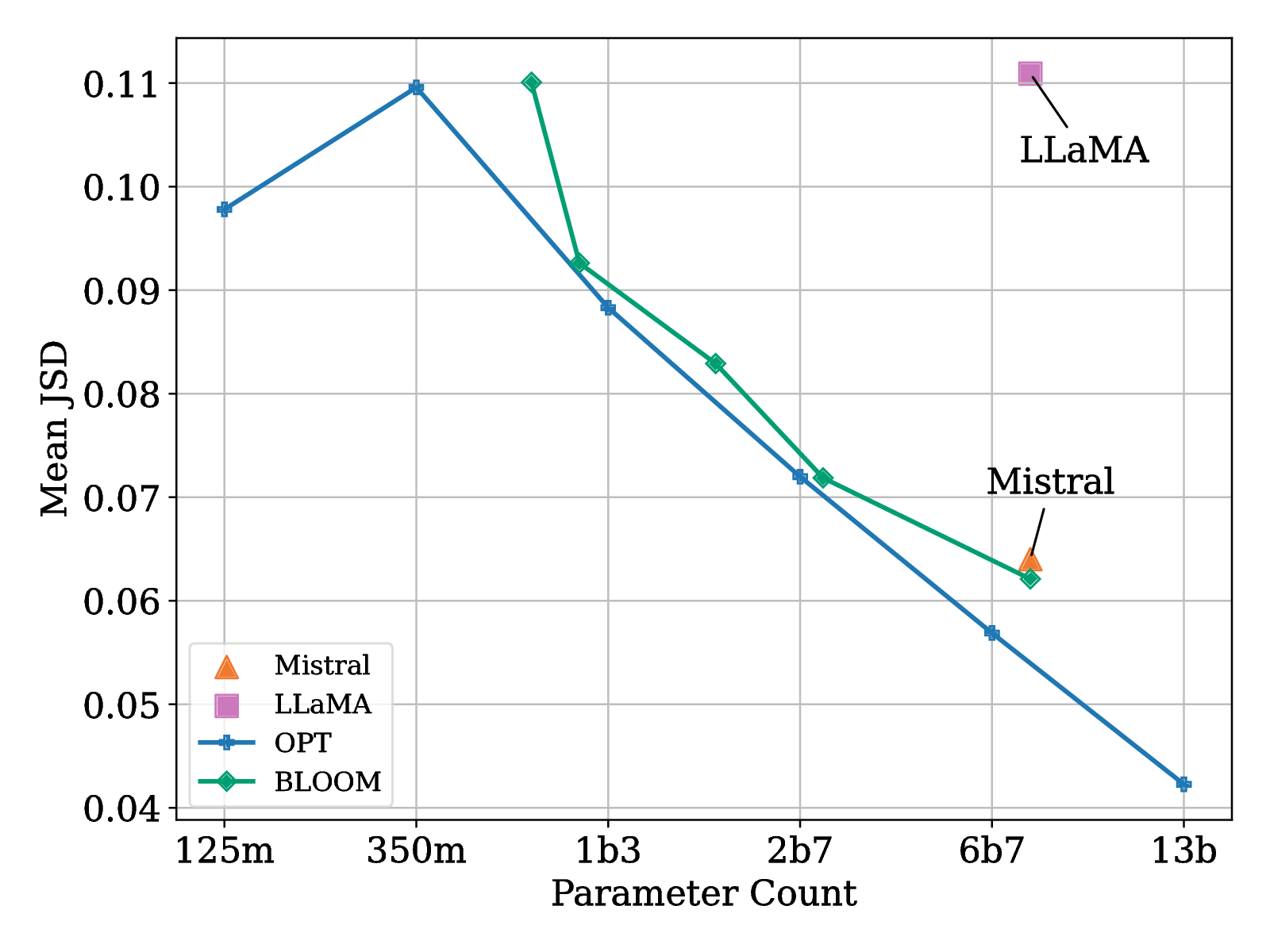
The distances between original and compressed LLMs decrease as the model size scales up
Conclusion
- In the paper, we have investigated the impact of quantization on the confidence and calibration of LLMs
- Quantization leads to an increase in calibration error and statistically significant changes in confidence levels for correct predictions
- We identify instances of confidence change occurring in data where models lack confidence before quantization
- Our findings provide insights into quantization loss and suggest a potential direction for future work, emphasizing the need to focus on calibrating LLMs, specifically on uncertain examples
Questions?
We released the code for reproducing the experiments [here]
Project website: https://www.anr-dike.fr